Nonlinear Structural Materials for Multiphysics Modeling
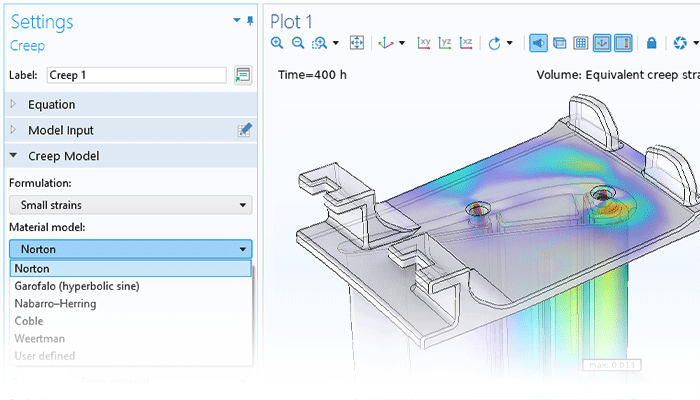
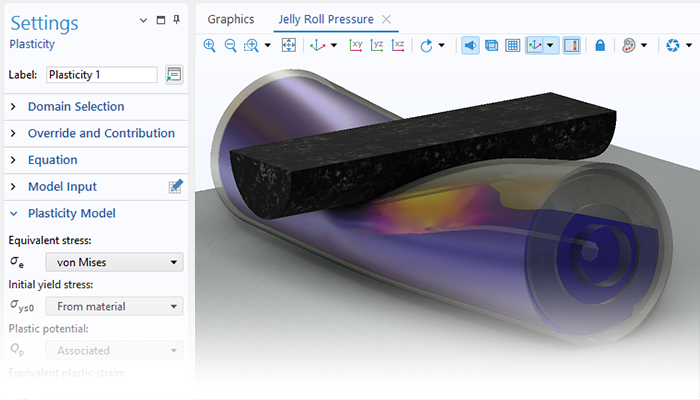
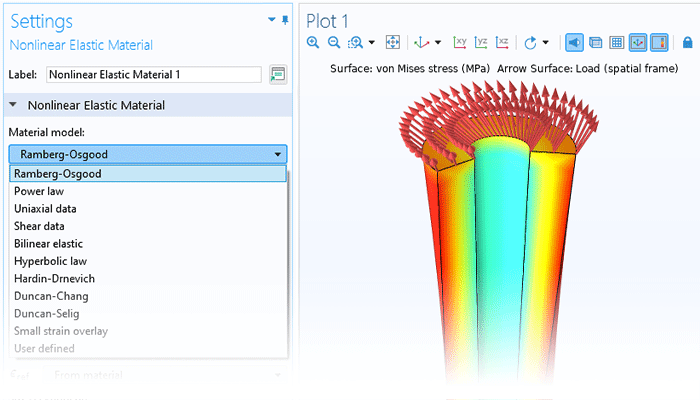
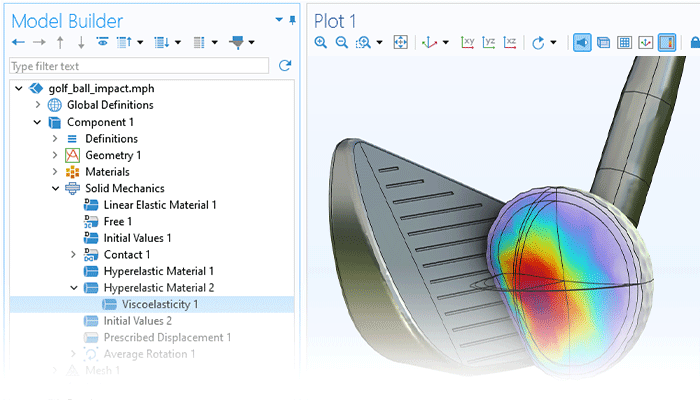
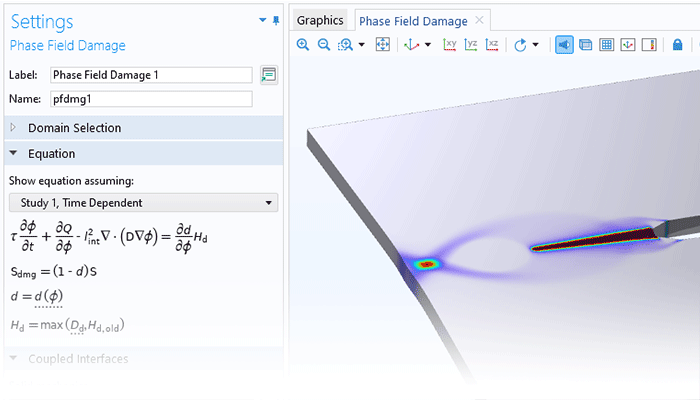
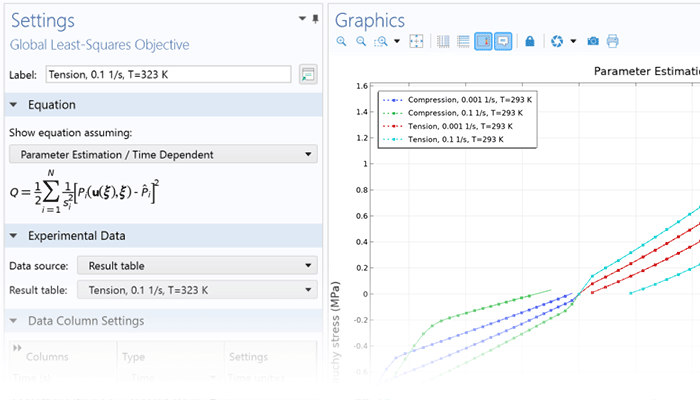
The functionality for modeling nonlinear materials augments all of the structural analyses available within the Structural Mechanics Module or the MEMS Module. Linear elastic, hyperelastic, or nonlinear elastic material models can be combined with nonlinear effects, such as plasticity, creep, viscoplasticity, or damage, and the versatility of the COMSOL Multiphysics® simulation software makes it easy to include multiphysics couplings with a couple of clicks. Users can define their own models based on, for example, stress or strain invariants and create their own flow rules, creep laws, and strain energy density functions for hyperelasticity.
Multiphysics capabilities are built into the COMSOL Multiphysics® software platform for modeling thermal expansion, pore pressure, fluid–structure interaction, and many more multiphysics phenomena. All of the structural materials included in the Nonlinear Structural Materials Module can be used in multiphysics analysis.