Model Optically Large Problems with the Beam Envelope Method
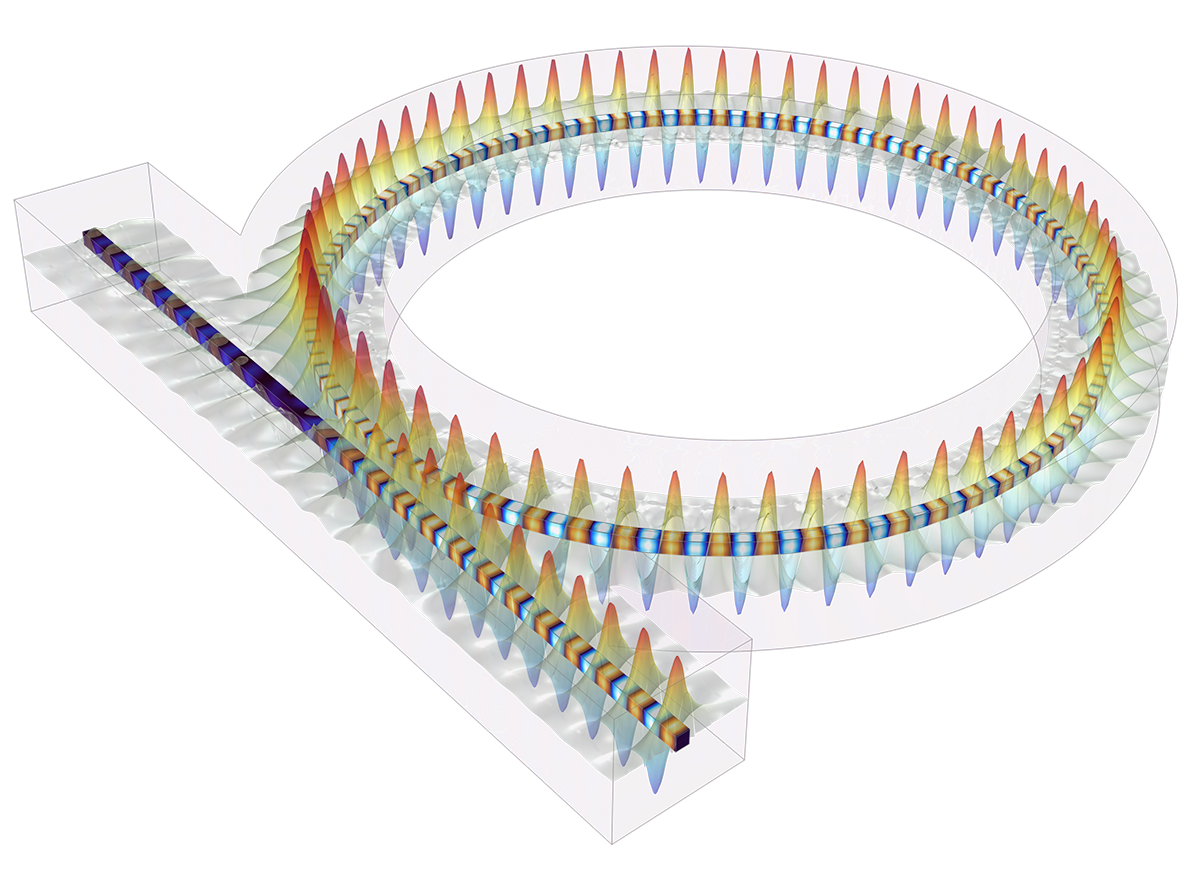
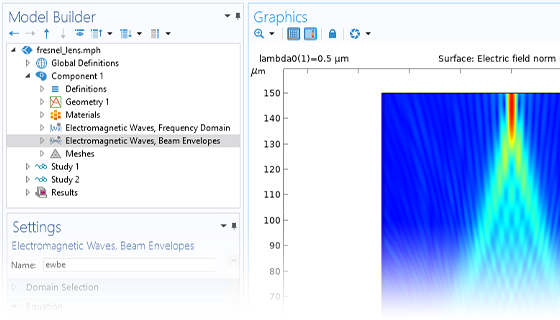
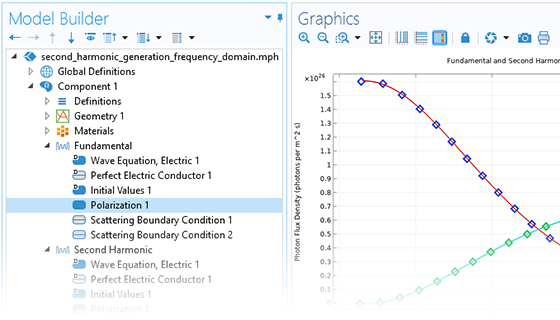
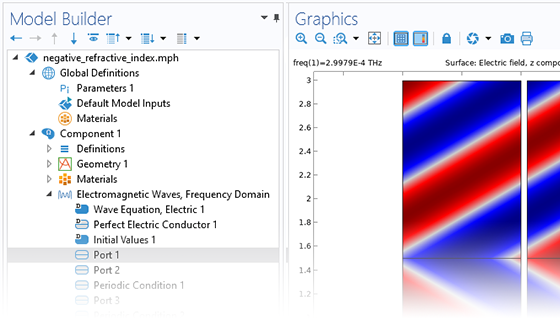
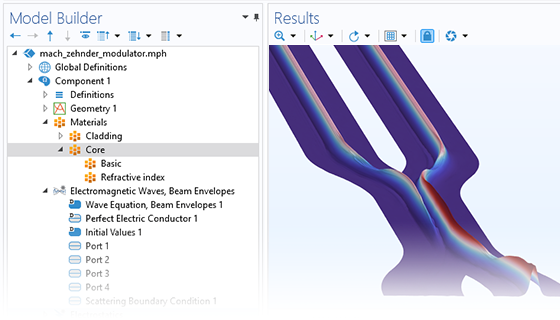
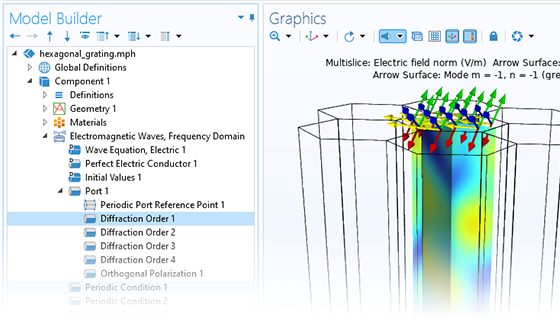
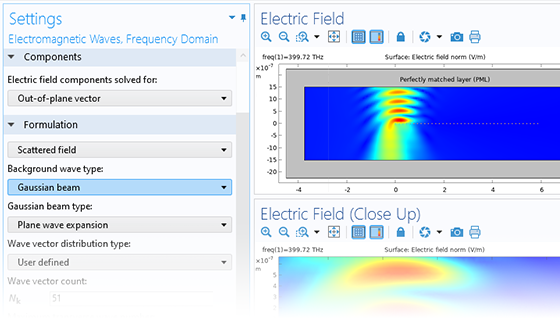
In addition to traditional numerical methods, the Wave Optics Module includes a specialized beam envelope method that can be used to simulate optically large devices with far fewer computational resources than conventional techniques. Applications include directional couplers, fiber Bragg gratings, lens systems, waveguides, external optical systems, fiber couplings, laser diode stacks, and laser beam delivery systems.
The beam envelope method analyzes the slowly varying electric field envelope for optically large simulations without relying on approximations. It requires much fewer mesh elements to resolve each propagating wave when compared to traditional methods.