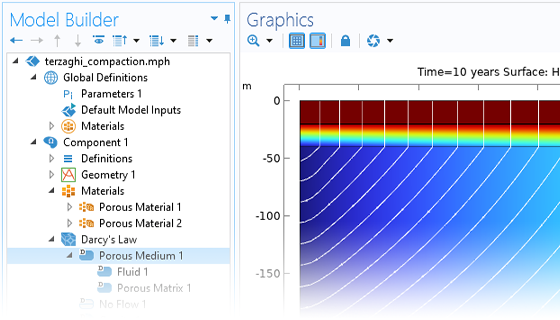
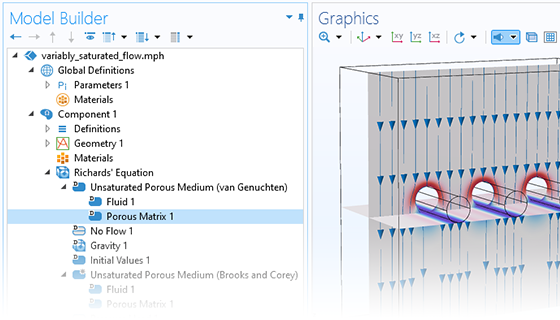
Subsurface Flow Affects Many Geophysical Properties
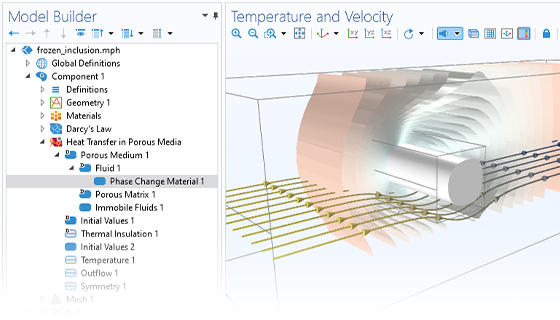
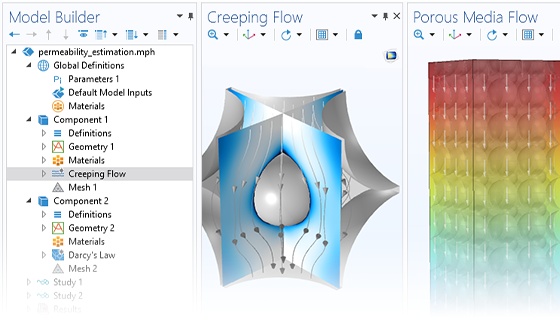
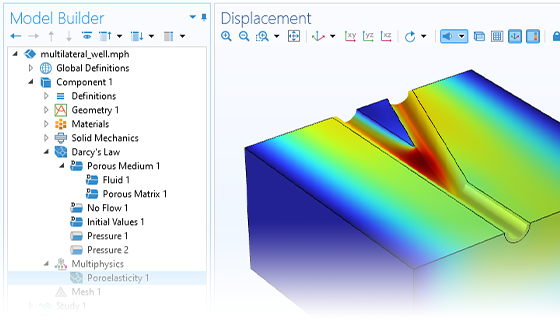
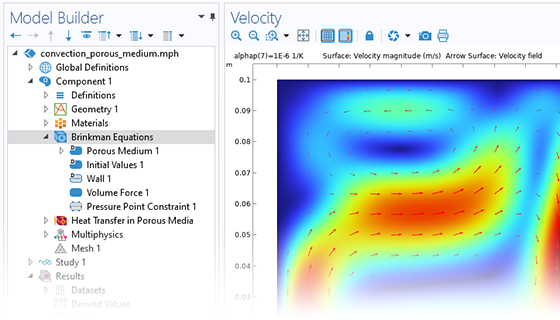
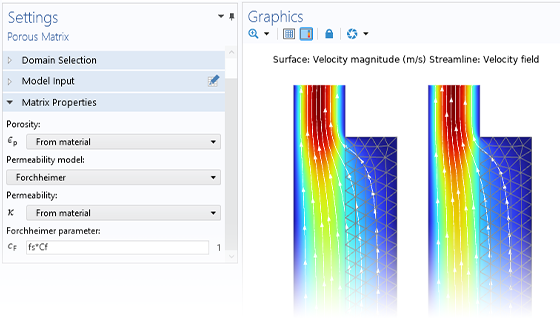
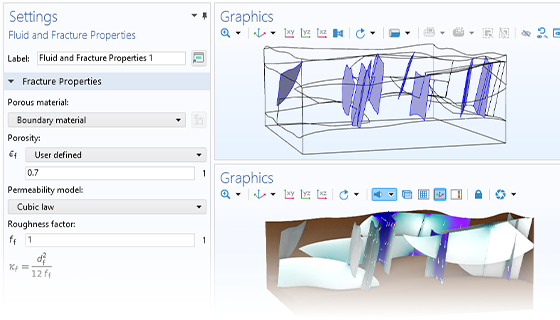
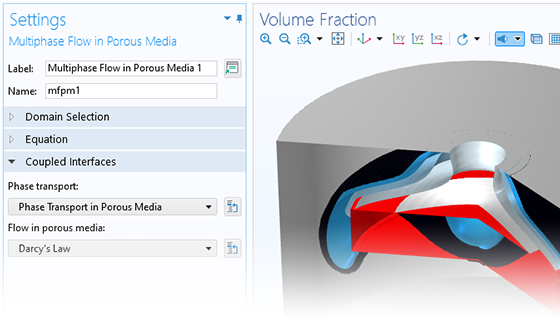
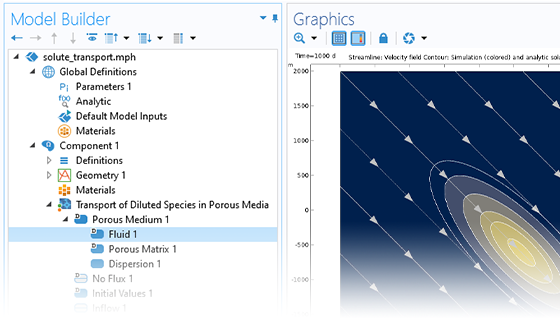
The need for advanced porous media modeling spans many industries and applications. The Subsurface Flow Module helps agricultural, civil, and environmental engineers and scientists across various industries analyze subsurface flows and optimize their designs and processes.
With COMSOL Multiphysics®, you can simulate the effects that porous media has on transport processes for hydrology, geotechnical applications, reservoir engineering, and environmental engineering. The software provides comprehensive modeling capabilities that automatically set up and solve the equations specific to the type of subsurface porous media flow being modeled.